 [STRAUS Applications] [STRAUS Specifications]
[STRAUS Applications] [STRAUS Specifications][STRAUS Users Page] [STRAUS Model Archive] [Technical Papers and Tips Contents Page]
[Technical Articles Contents Page] [Home Page] [Previous Page] [Next Page]
 [STRAUS Applications] [STRAUS Specifications]
[STRAUS Applications] [STRAUS Specifications]
[STRAUS Users Page] [STRAUS
Model Archive] [Technical Papers and Tips
Contents Page]
[Technical Articles
Contents Page] [Home Page] [Previous
Page] [Next Page]

When modelling symmetric structures it is common practice to reduce the size of the model by invoking the principle of symmetry. Appropriate freedom conditions are applied on the plane of symmetry so that the half of the structure modelled behaves as though it is still attached to the other half of the structure.
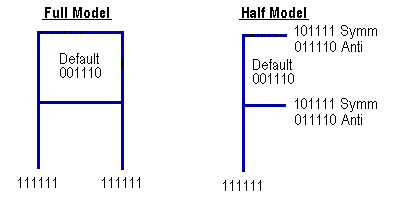
The nature of a symmetry boundary condition means that a structure must deform symmetrically about the plane of symmetry. This normally means that in addition to the structural geometry being symmetric the loading must also be symmetric. Whilst most analysts are comfortable with the concept of symmetry in linear static problems, experience shows that this is not necessarily the case with regard to natural frequency and buckling analysis.
Symmetric half models can be used for buckling and natural frequency analysis but this is not as straight forward as it is for linear static analysis.
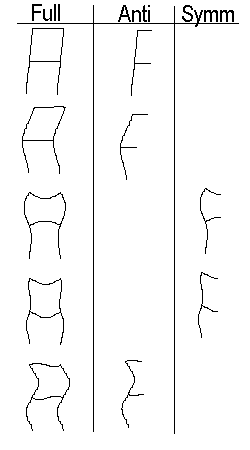
A symmetry model with symmetric boundary conditions will yield the symmetric buckling and vibration modes only. To obtain the antisymmetric modes it will be necessary to run the model a second time with antisymmetric boundary conditions applied to the geometric symmetry plane of the structure. For large models it may be better to use the symmetry approach, since running the half model twice will usually be faster than running the full model once.
Antisymmetric boundary conditions are simply the opposite of symmetric conditions - any degrees of freedom that were fixed in the symmetric case are now free and those degrees of freedom that were free are now fixed.
The following example shows this. Both a symmetric and an antisymmetric model are run and the results compared with a full model. The table contains the natural frequencies whilst the figures show the first 10 modes.
| Full Model | Symmetric Model | Antisymmetric Model |
|---|---|---|
| 17.24 | 125.04 | 17.34 |
| 56.94 | 0 | 56.94 |
| 125.04 | 125.04 | 0 |
| 175.18 | 175.18 | 0 |
| 195.97 | 0 | 195.97 |
| 254.95 | 254.95 | 0 |
| 258.08 | 258.08 | 0 |
| 291.29 | 291.29 | 0 |
| 457.03 | 0 | 457.03 |
| 560.78 | 560.78 | 0 |
For more information please contact us by
e-mail: hsh@iperv.it