 [STRAUS Applications] [STRAUS Specifications]
[STRAUS Applications] [STRAUS Specifications] [STRAUS Users Page] [STRAUS Model Archive] [Technical Papers and Tips Contents Page]
[Technical Articles Contents Page] [Home Page] [Previous Page] [Next Page]
 [STRAUS Applications] [STRAUS Specifications]
[STRAUS Applications] [STRAUS Specifications]
[STRAUS Users Page] [STRAUS
Model Archive] [Technical Papers and Tips
Contents Page]
[Technical Articles
Contents Page] [Home Page] [Previous
Page] [Next Page]

We get lots of questions from users regarding the use of damping in dynamic analysis. The most common question is what values of damping should be used in a particular problem. This is difficult to answer. The factors that influence damping are complex and model dependent and thus it is not possible to provide users with a definitive answer. The following discussion should provide the necessary background for users to determine an acceptable value of damping for most applications.
Typical published values of damping are:
| Continuous Metal Structures | 2% - 4% |
| Jointed (Bolted) Structures | 4% - 7% |
| Prestressed Concrete Structures | 2% - 5% |
| Reinforced Concrete Structures | 4% - 7% |
| Small Diameter Piping Systems | 1% - 2% |
| Equipment/Large Diameter Pipes | 2% - 3% |
These figures are given as a percentage of critical damping. Critical damping is the amount of damping which will cause a vibrating structure to reach an equilibrium state in the shortest possible time; that is, without any oscillatory behaviour.
Only a broad range of damping can be given for each type of structure since there are many factors and design details that influence the damping. Also the damping characteristics of a structure are often nonlinear. The lower values of damping may occur when the structure undergoes small deflections at low levels of stress. At higher levels of stress and larger vibration amplitudes the damping may be at the upper end of the range given.
Using values of damping from reference texts is at best approximate. The acceptability of using such values really depends on the analysis being carried out.
In some cases the magnitude of damping is not significant. An example is a simple harmonic analysis in which the response is to be determined at some excitation frequency between two of the natural frequencies. This can be seen in figure 8. The value of damping ratio used will have almost no effect on the results and published values of damping ratio should be sufficient.
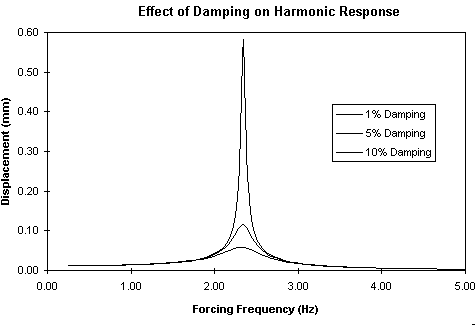
Effect of Damping on Dynamic Response
In other cases we may wish to calculate the response at or near resonance; that is the response when the structure is excited at or near its natural frequency. In this case the magnitude of the response is controlled solely by damping. Once again this can be seen in figure 8. If a structure has zero damping the resonant response will be infinite. If you are trying to calculate the response in a resonant condition then values of damping obtained from books will not be sufficiently accurate. It will be necessary to measure the actual damping ratio by experiment on the real structure. Methods by which the damping can be measured experimentally are covered in most dynamics books.
In most dynamic analysis work published damping ratios are of sufficient accuracy since it is rare to design structures that operate at or close to the resonant frequency. However, published values should not be used blindly. Some attempt should be made to establish their source and to make a qualitative judgement on which value, within the given range is applicable to the structure in question.
If the analysis is such that published damping ratios can be used, it is a good idea to do a sensitivity study, to assess the likely error resulting from inaccuracies in the assumed damping ratio. Several runs should be made with values of damping spread over the range given in the texts and the effect of this on the response assessed. If the response varies greatly, this is an indication that the damping should be experimentally determined.
Considerable judgement is required by the user in the choice of the damping ratio. The value used depends on the design, loading and vibration modes of the structure.
For more information please contact us by
e-mail: hsh@iperv.it