DOCUMENTAZIONE TECNICA
CODICE DI CALCOLO STRAUS
ESEMPIO DI CALCOLAZIONE TIPO
CARICO CRITICO IN PILASTRI
A SEZIONE COMPLETAMENTE REAGENTE
Prof. Antonio Casellato
Universita' di Padova
0. Generalità
.Schematizzato il pilastro con un elemento monodomensionale (beam) diviso in vai tronchi con il presente calcolo si intende analizzare la precisione di calcolo che si può ottenere considerando la struttura divisa in un numero variabile di tronchi.
Per semplicità di calcolo si prende in esame un pilastro incastrato alla base e libero in sommità: i risultati che ne conseguono e la metodologia di analisi si possono ritenere indicativi anche per casi diversi e più generali per condizioni di carico e/o di vincolo.
.
1. Calcolo teorico
.pilastro a base quadrata con lato di 50 cm,
altezza complessiva pari a 10,00 m,
incastro alla base e libero in sommità.
materiale: calcestruzzo con sezione interamente reagente,
modulo di elasticità E = 30000 MPa.
Calcolo analitico del carico critico:
Il carico euleriano risulta: NE = 3855,314 kN.
2. Calcolo con il programma Straus7.
Il calcolo, non lineare per geometria della struttura, viene effettuato per successivi incrementi di carico a partire da una situazione perturbata per effetto di una forza orizzontale trascurabile.
Le forze base considerate (forze che saranno moltiplicate per il coefficiente di incremento sono:
Forza orizzontale: F = 1 N,
Carico verticale: N = 1000000 N.
2.1. MODELLO n° 1:
Il pilastro viene diviso in 2 tronchi di eguale lunghezza
Vengono qui di seguito riportati i diagrammi. numero di incrementi – spostamento orizzontale della sommità del pilastro.
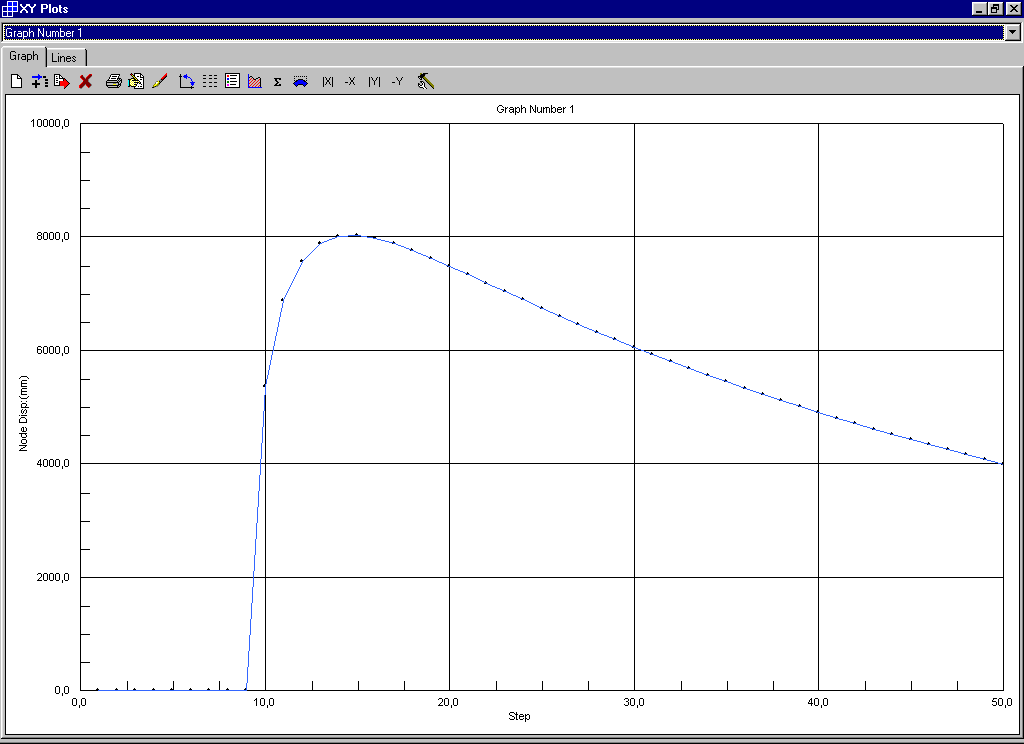
Con incrementi di carico da 0 a 24,5 con passo pari a 0,5 si ottiene:

Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè al nono incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 4.
Si ha allora:
4,0 MN < Pcr < 4,5 MN.
Un primo affinamento del calcolo si ottiene con incrementi di carico da 3,80 a 4,78 e con passo pari a 0,02 si ottiene così:
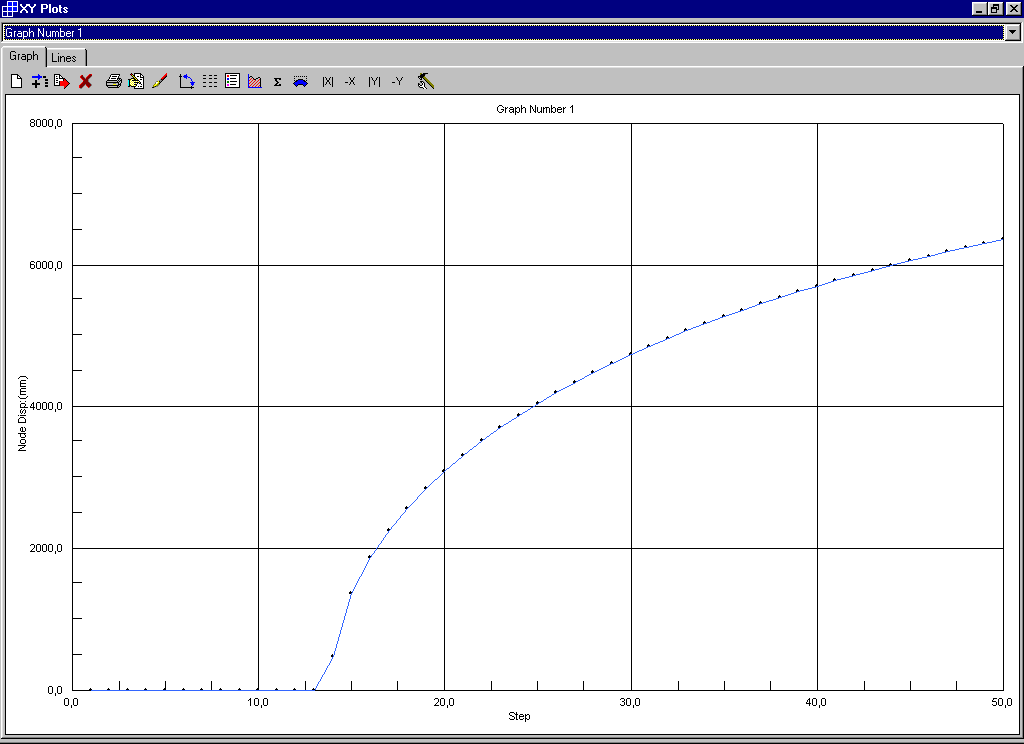
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè al quattordicesimo incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 4,06.
Si ha allora:
4,06 MN < Pcr < 4,08 MN.
Con incrementi di carico da 4,000 a 4,245 con passo pari a 0,005 si ottiene:
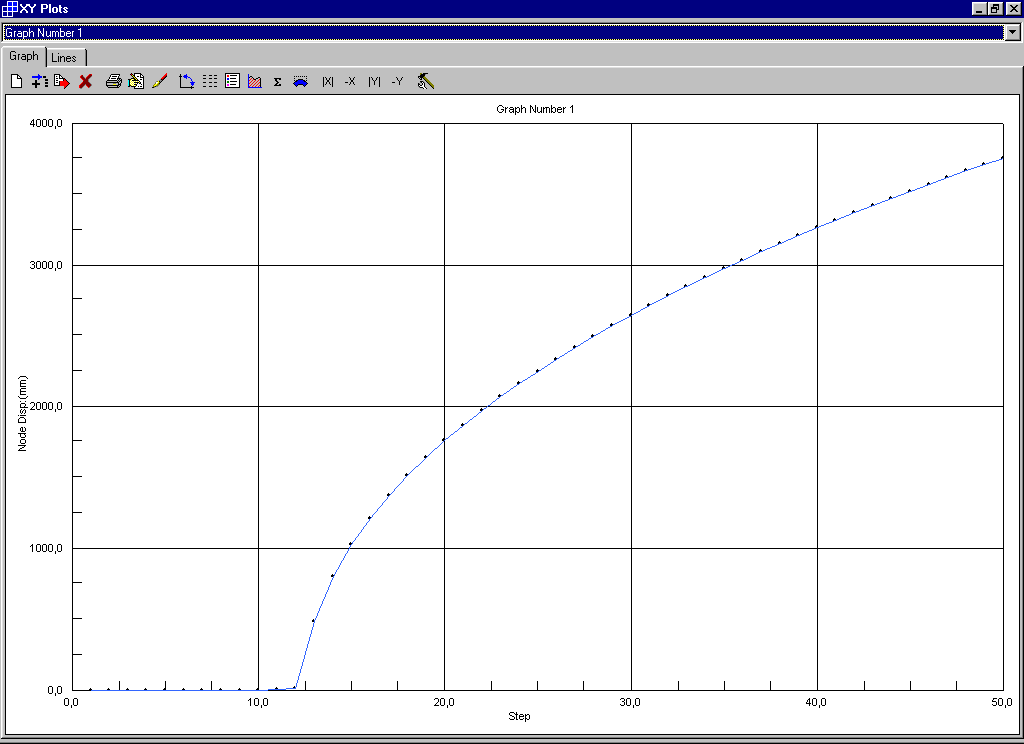
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè al dodicesimo incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 4,060.
Si ha allora:
4,060 MN < Pcr < 4,065 MN.
2.2. MODELLO n° 2:
Il pilastro viene diviso in 10 tronchi di eguale lunghezza
Vengono qui di seguito riportati i diagrammi. numero di incrementi – spostamento orizzontale sommità del pilastro.
Con incrementi di carico da 0 a 24,5 con passo pari a 0,5 si ottiene:
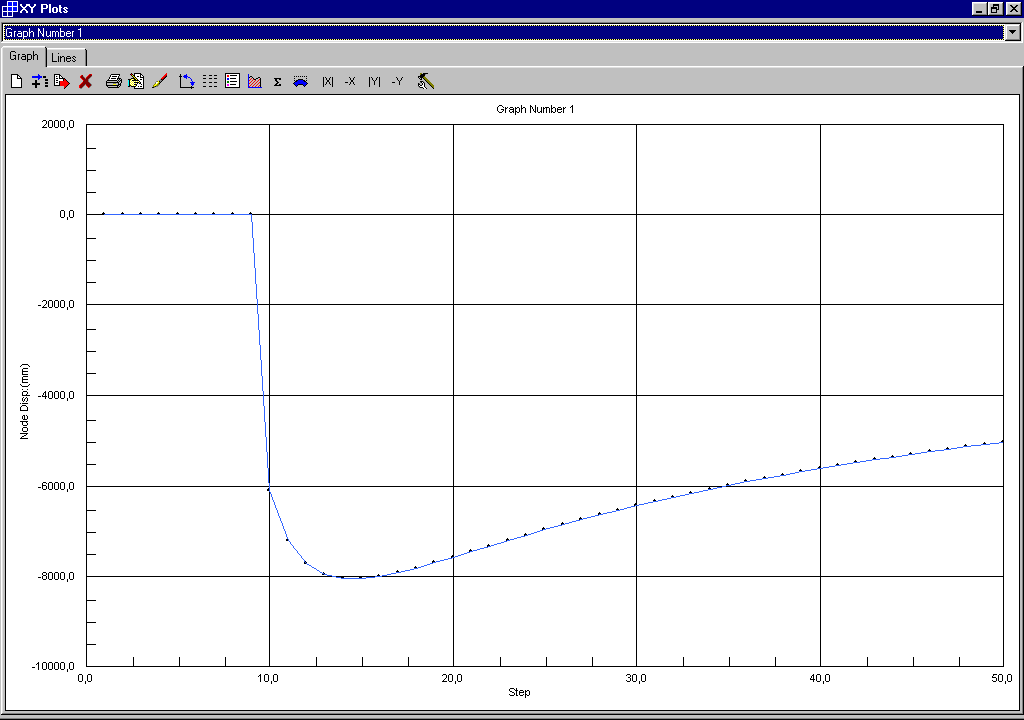
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè al nono incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 4.
Si ha allora:
4,0 MN < Pcr < 4,5 MN.
Con incrementi di carico da 3,80 a 4,78 con passo pari a 0,02 si ottiene:
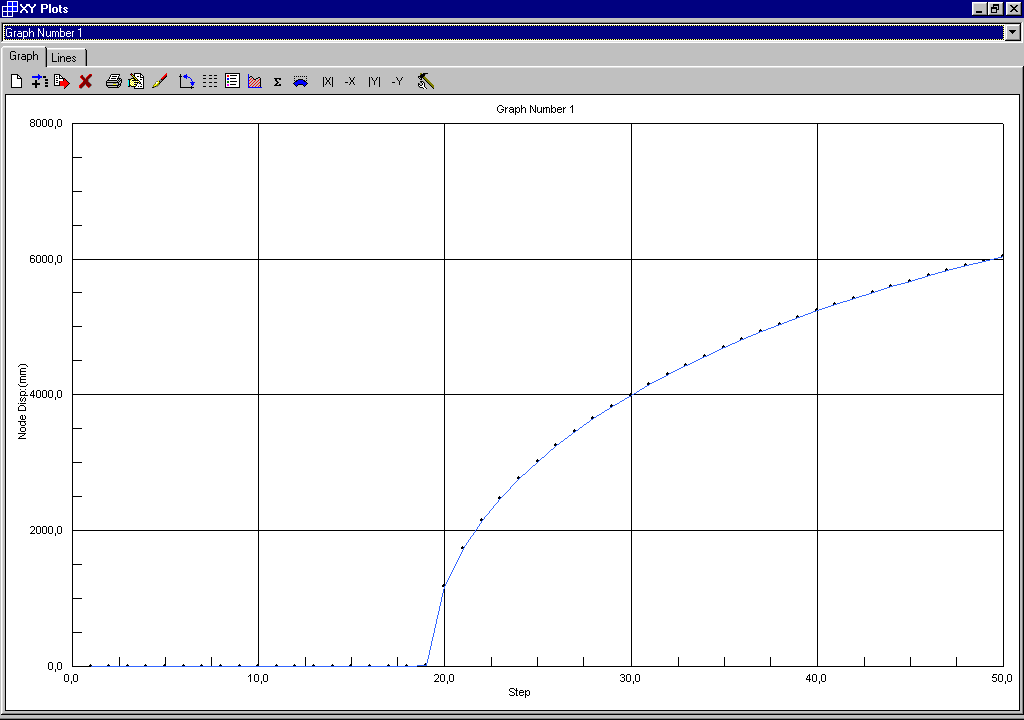
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè al diciannovesimo incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 3,86.
Si ha allora:
3,86 MN < Pcr < 3,88 MN.
Con incrementi di carico da 4,000 a 4,245 con passo pari a 0,005 si ottiene:
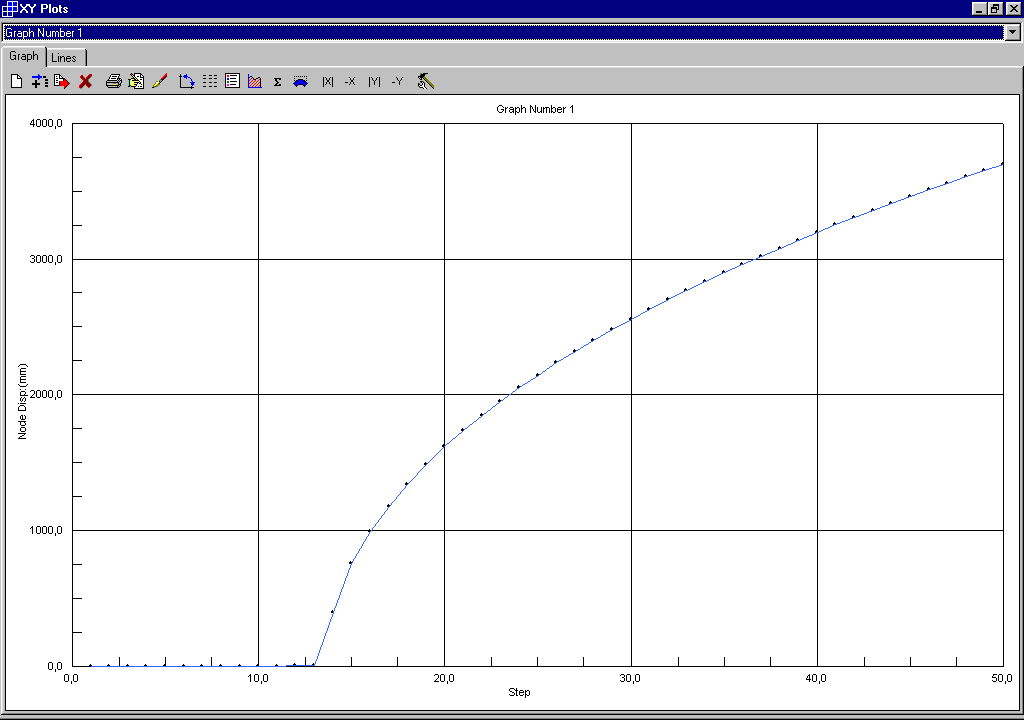
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè al tredicesimo incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 3.860.
Si ha allora:
3,860 MN < Pcr < 3,65 MN.
2.3. MODELLO n° 3:
Il pilastro viene diviso in 100 tronchi di eguale lunghezza
Vengono qui di seguito riportati i diagrammi. numero di incrementi – spostamento orizzontale sommità del pilastro.
Con incrementi di carico da 0 a 24,5 con passo pari a 0,5 si ottiene:
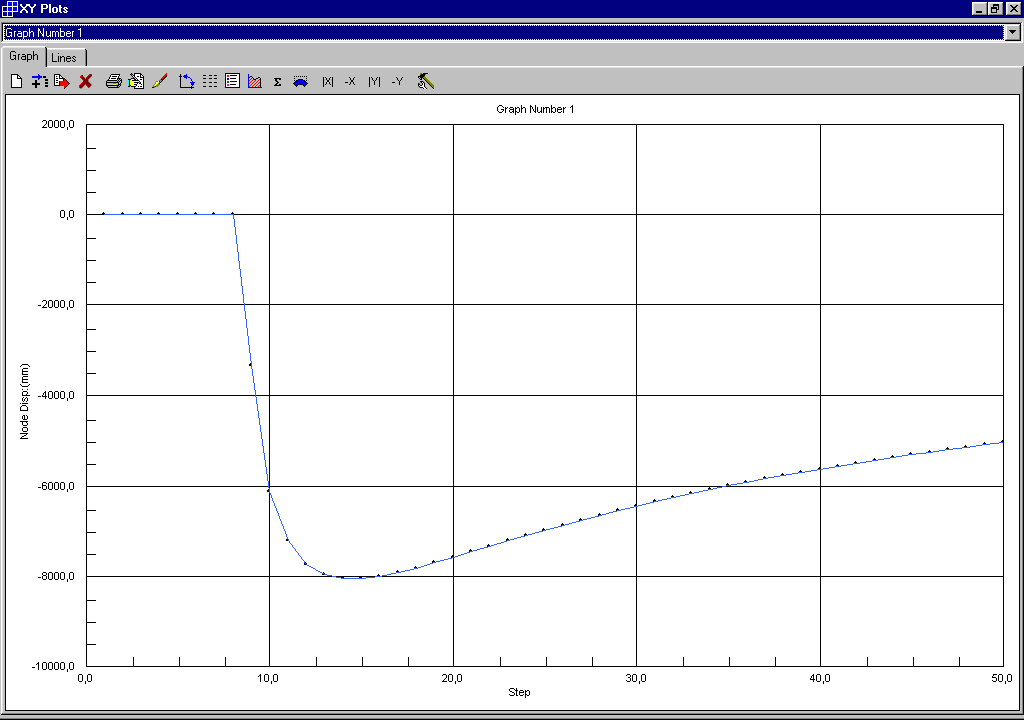
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè all’ottavo incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 4.
Si ha allora:
3,5 MN < Pcr < 4,0 MN.
Con incrementi di carico da 3,80 a 4,78 con passo pari a 0,02 si ottiene:
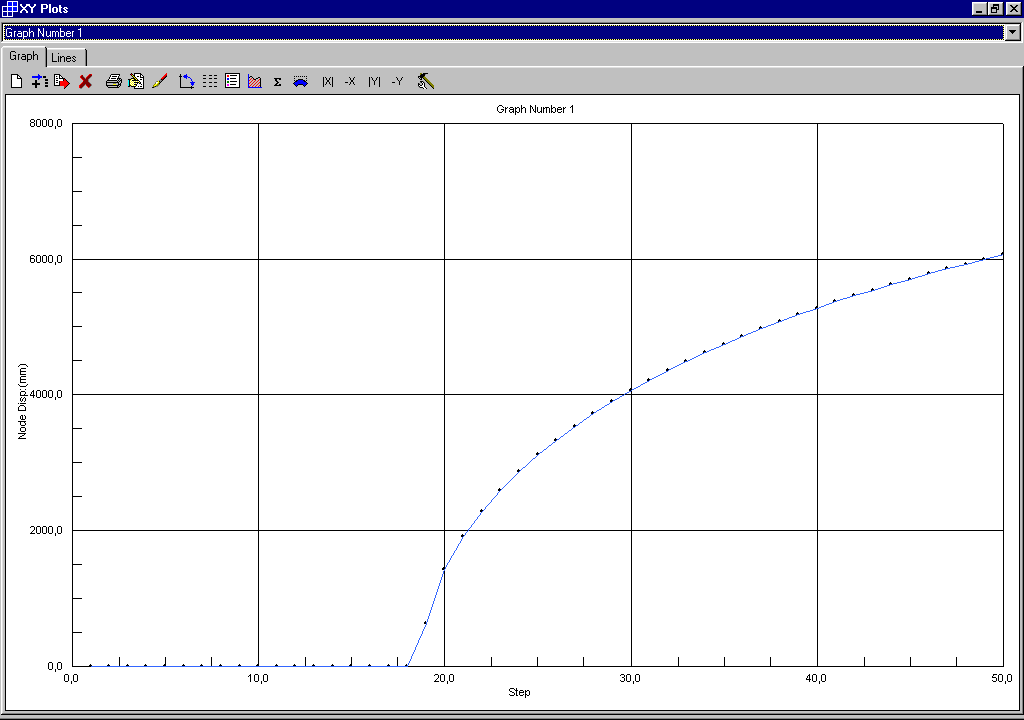
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè al diciottesicesimo incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 3,84.
Si ha allora:
3,84 MN < Pcr < 3,86 MN.
Con incrementi di carico da 4,000 a 4,245 con passo pari a 0,005 si ottiene:
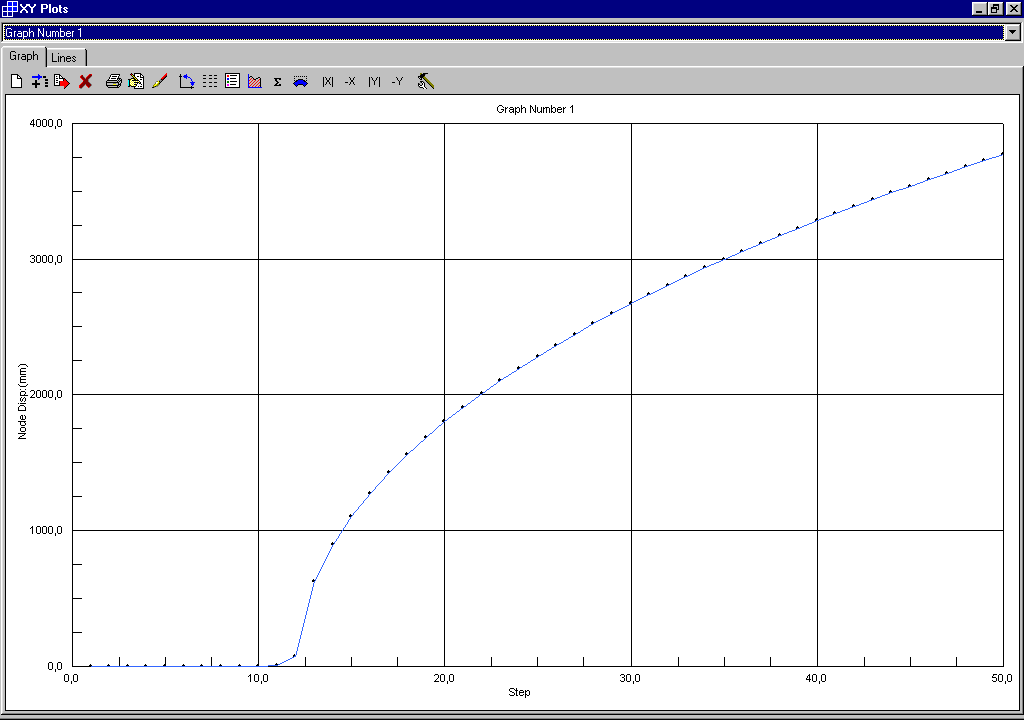
Il carico critico si ha in corrispondenza dell’improvviso aumento di deformazione e cioè all’undicesimo incremento di carico cui corrisponde un coefficiente di amplificazione con valore pari a 3,850.
Si ha allora:
3,850 MN < Pcr < 3,855 MN.